Tutorial - A Diffusion Model for Image Restoration
Theoretical Foundations of SDE-Based Diffusion Models for Image Restoration
Introduction
In this post, we talk about generative models for image restoration, taking Image Restoration with Mean-Reverting Stochastic Differential Equations (IR-SDE)
Background of Score-based Diffusion Models through SDEs
First, let’s briefly review the basic framework of score-based diffusion models. Let $\mathbf{x}_0 \sim p_0(\mathbf{x})$ denote a sample $\mathbf{x}_0 \in \mathbb{R}^d$ drawn from the initial ground truth data distribution $p_0(\mathbf{x})$. After adding a small amount of noise to $\mathbf{x}_0$, we have a slightly noise-perturbed sample $\mathbf{x}_1 \in \mathbb{R}^d$. By repeating this step for $N$ (e.g., $N$ could be thousands) steps, we obtain a sequence of noisy samples $\{ \mathbf{x}_i \}_{i=0}^N \in \mathbb{R}^d$ indexed by the step variable $i$.
Generalizing the discrete step variable $i$ to a continuous time variable $t$, we have a continuous forward diffusion process $\{ \mathbf{x}(t) \}_{t=0}^T \in \mathbb{R}^d$. With sufficiently large $T$, $\mathbf{x}(T)$ is completely noisy without any information about the initial data $\mathbf{x}(0)$.

Note that the initial data distribution $p_0(\mathbf{x})$ is often intractable. However, given a well-defined forward diffusion process, the final noisy sample distribution $\mathbf{x}(T) \sim p_T(\mathbf{x})$ can be in a tractable form (e.g., a standard Gaussian distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$).
To generate samples from such an intractable data distribution $p_0(\mathbf{x})$, a potential way is to reverse the forward diffusion process such that we sample $\mathbf{x}(T)$ from a tractable prior distribution $p_T(\mathbf{x})$, then generate intermediate noisy data $\mathbf{x}(t) \sim p_t(\mathbf{x})$, and finally the clean data $\mathbf{x}(0) \sim p_0(\mathbf{x})$ through a tractable reverse diffusion process running backwards in time, $T \to 0$.
In order to achieve this goal, we often start with a tractable prior distribution $p_T(\mathbf{x})$ (e.g., a standard Gaussian distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$). The forward diffusion process is modeled by a stochastic differential equation (SDE) to perturbe data such that the final output will end up being completely noisy and follow the prior distribution $p_T(\mathbf{x})$.
Formally, the SDE for the forward diffusion process can be constructed in the form of:
\begin{equation} \label{eq:forward} \mathrm{d} \mathbf{x} = \mathbf{f}(\mathbf{x}, t) \mathrm{d} t + g(t)\mathrm{d} \mathbf{w} \end{equation}
where $\mathbf{w}$ is the standard Wiener process (a.k.a., Brownian motion) (time flow: $0 \to T$), $\mathrm{d}t$ is an infinitesimal positive time interval, and $f(\mathbf{x}, t)$ and $g(t)$ are called the drift and diffusion coefficients of $\mathbf{x}$, respectively. Solving the above forward SDE, the intermediate noise-perturbed sample $\mathbf{x}(t)$ can be obtained given the initial data sample $\mathbf{x}(0)$.
Note that, the actual SDE can be in different forms such that the prior distribution $p_T(\mathbf{x})$ will have different forms, rather than just limited to standard Gaussiance distribution $\mathcal{N}(\mathbf{0}, \mathbf{I})$. However, we do not have to solve the forward SDE as our goal is to reverse the forward diffusion process or the SDE for generating data $\mathbf{x}(0)$ starting from the noise/prior $\mathbf{x}(T) \sim p_T(\mathbf{x})$:
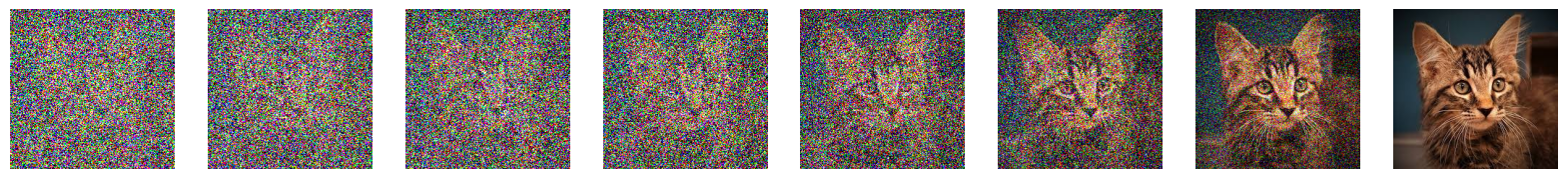
An important property of the diffusion process modeled by the above SDE (Eq. \eqref{eq:forward}): its reverse process running backwards in time is also a diffusion process modeled by a reverse-time SDE corresponding to the forward SDE.
\begin{equation} \label{eq:reverse} \mathrm{d}\mathbf{x} = [ \mathbf{f}(\mathbf{x}, t) - g(t)^2 \underbrace{ \nabla_{\mathbf{x}}\log{p_t(\mathbf{x})} }_{\text{score: } s_{\theta}(\mathbf{x}, t)} ] \mathrm{d}t + g(t)\mathrm{d}\mathbf{\bar{w}} \end{equation}
where $\mathbf{\bar{w}}$ is a standard reverse-time Wiener process (time flow: $T \to 0$), $\mathrm{d}t$ is an infinitesimal negative time interval, and $s_{\theta}(\mathbf{x}, t)=\nabla_{\mathbf{x}}\log{p_t(\mathbf{x})}$ is called the score of the marginal distribution $p_t(\mathbf{x})$ for $\mathbf{x}(t)$ at time $t$. Note that the score function $s_{\theta}(\mathbf{x}, t)$ is often intractable and needs to be approximated by a neural network learned from data.
Image Restoration with Mean-reverting SDE
In diffusion models, given a sample from the prior distribution, $\mathbf{x}(T) \sim p_T(\mathbf{x})$, we can generate data from the data distribution, $\mathbf{x}(0) \sim p_0(\mathbf{x})$, through the reverse-time SDE. In the problem of image restoration, given the low-quality (LQ) data (e.g., low-resolution images), the goal is to generate high-quality (HQ) data (e.g., high-resolution images). Corresponding to the framework of the SDE-based diffusion processes, we have:
- LQ: known prior distribution, $\mathbf{x}(T) \sim p_T(\mathbf{x})$,
- HQ: unknown data distribution, $\mathbf{x}(0) \sim p_0(\mathbf{x})$
Mean-reverting SDE
To adapt to the SDE-based diffusion model framework, we need to design a SDE that perturbes the HQ sample $\mathbf{x}(0)$ such that the final noisy counterpart $\mathbf{x}(T)$ follow the same distribution of LQ data.
A special form of the forward SDE
We have a special SDE:
\[\begin{equation} \label{eq:irsde} \mathrm{d}\mathbf{x} = \theta_t(\boldsymbol{\mu} - \mathbf{x}) \mathrm{d}t + \sigma_t \mathrm{d} \mathbf{w} \end{equation}\]where \(\mu\) is the LQ sample, $\theta_t$ and $\sigma_t$ are time-dependent hyperparameters. To sovle the SDE (Eq. \eqref{eq:irsde}), let’s first define a function
\[\begin{equation} \phi(\mathbf{x}, t) = \mathbf{x} \mathrm{e}^{\bar{\theta}_t} \end{equation}\]where $\mathbf{x}(t) \sim p_t(\mathbf{x})$ is the data sample at time $t$ and $\bar{\theta}_t=\int_0^t \theta_z \mathrm{d}z$. We can get the differential equation of $\phi(\mathbf{x}, t)$:
\[\begin{equation} \mathrm{d} \phi(\mathbf{x}, t) = \mathbf{x} \mathrm{e}^{\bar{\theta}_t} \frac{\partial \bar{\theta}_t}{\partial t} \mathrm{d}t + \mathrm{e}^{\bar{\theta}_t} \mathrm{d} \mathbf{x} \end{equation}\]Note that $\bar{\theta}_t=\int_0^t \theta_z \mathrm{d}z$, $\frac{\partial \bar{\theta}_t}{\partial t} = \theta_t$. Also substituting $\mathrm{d} \mathbf{x}$ with Eq. \eqref{eq:irsde}, we have
\[\begin{equation} \begin{aligned} \mathrm{d} \phi(\mathbf{x}, t) &= \mathbf{x} \mathrm{e}^{\bar{\theta}_t} \frac{\partial \bar{\theta}_t}{\partial t} \mathrm{d}t + \mathrm{e}^{\bar{\theta}_t} \mathrm{d} \mathbf{x} \\ &= \mathbf{x} \mathrm{e}^{\bar{\theta}_t} \theta_t \mathrm{d}t + \mathrm{e}^{\bar{\theta}_t} [ \theta_t(\boldsymbol{\mu} - \mathbf{x}) \mathrm{d}t + \sigma_t \mathrm{d} \mathbf{w}_t] \\ &= [\cancel{\mathbf{x} \theta_t \mathrm{e}^{\bar{\theta}_t}} + \boldsymbol{\mu} \theta_t \mathrm{e}^{\bar{\theta}_t} - \cancel{\mathbf{x} \theta_t \mathrm{e}^{\bar{\theta}_t}}] \mathrm{d}t + \sigma_t \mathrm{e}^{\bar{\theta}_t} \mathrm{d} \mathbf{w}_t \\ &= \boldsymbol{\mu} \theta_t \mathrm{e}^{\bar{\theta}_t} \mathrm{d}t + \sigma_t \mathrm{e}^{\bar{\theta}_t} \mathrm{d} \mathbf{w}_t \end{aligned} \end{equation}\]where we change $\mathbf{w}$ to $\mathbf{w}_t$ to explicitly express its change over time $t$. As such, we have the relationship between $\phi(\mathbf{x}, t)$ and $\phi(\mathbf{x}, s)$ at any two different times $s < t$:
\[\begin{equation} \begin{aligned} \phi(\mathbf{x}, t) - \phi(\mathbf{x}, s) &= \int_s^t \mathrm{d} \phi(\mathbf{x}, z) \\ &= \int_s^t (\boldsymbol{\mu} \theta_z \mathrm{e}^{\bar{\theta}_z} \mathrm{d}z + \sigma_z \mathrm{e}^{\bar{\theta}_z} \mathrm{d} \mathbf{w}_z) \\ &= \int_s^t \boldsymbol{\mu} \theta_z \mathrm{e}^{\bar{\theta}_z} \mathrm{d}z + \int_s^t \sigma_z \mathrm{e}^{\bar{\theta}_z} \mathrm{d} \mathbf{w}_z \\ \end{aligned} \end{equation}\]Substitute $\phi(\mathbf{x}, t)$ with $\mathbf{x} \mathrm{e}^{\bar{\theta}_t}$ and divide both sides of the above equation by $\mathrm{e}^{\bar{\theta}_t}$, we have
\[\begin{equation} \label{eq:xts} \begin{aligned} \mathbf{x}(t) \mathrm{e}^{\bar{\theta}_t} - \mathbf{x}(s) \mathrm{e}^{\bar{\theta}_s} &= \int_s^t \boldsymbol{\mu} \theta_z \mathrm{e}^{\bar{\theta}_z} \mathrm{d}z + \int_s^t \sigma_z \mathrm{e}^{\bar{\theta}_z} \mathrm{d} \mathbf{w}_z \\ \Longrightarrow \mathbf{x}(t) - \mathbf{x}(s) \mathrm{e}^{\bar{\theta}_s - \bar{\theta}_t} &= \int_s^t \boldsymbol{\mu} \theta_z \mathrm{e}^{\bar{\theta}_z - \bar{\theta}_t} \mathrm{d}z + \int_s^t \sigma_z \mathrm{e}^{\bar{\theta}_z - \bar{\theta}_t} \mathrm{d} \mathbf{w}_z \end{aligned} \end{equation}\]Recall that $\bar{\theta}_t=\int_0^t \theta_z \mathrm{d}z$. Given $0 < s < t$, we have
\[\begin{equation} \begin{aligned} \mathrm{e}^{\bar{\theta}_s - \bar{\theta}_t} &= \mathrm{e}^{\int_0^s \theta_z \mathrm{d}z - \int_0^t \theta_z \mathrm{d}z} \\ &= \mathrm{e}^{-\int_s^t \theta_z \mathrm{d}z}\\ & = \mathrm{e}^{-\bar{\theta}_{s:t}} \end{aligned} \end{equation}\]Rewriting the above Eq. \eqref{eq:xts}, we obtain
\[\begin{equation} \begin{aligned} \mathbf{x}(t) - \mathbf{x}(s) \mathrm{e}^{-\bar{\theta}_{s:t}} &= \int_s^t \boldsymbol{\mu} \theta_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d}z + \int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \end{aligned} \end{equation}\]Note that $\mathrm{d}(-\bar{\theta}_{z:t}) = \mathrm{d} (-\int_z^t \theta_z \mathrm{d}z) = \theta_z$
\[\begin{equation} \int_s^t \boldsymbol{\mu} \theta_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d}z = \boldsymbol{\mu} \mathrm{e}^{-\bar{\theta}_{z:t}} \bigg|_s^t = \boldsymbol{\mu} (\mathrm{e}^{-\bar{\theta}_{t:t}} - \mathrm{e}^{-\bar{\theta}_{s:t}}) = \boldsymbol{\mu} (1-\mathrm{e}^{-\bar{\theta}_{s:t}}) \end{equation}\] \[\begin{equation} \label{eq:solution_irsde} \begin{aligned} \mathbf{x}(t) &= \mathbf{x}(s) \mathrm{e}^{-\bar{\theta}_{s:t}} + \boldsymbol{\mu} (1-\mathrm{e}^{-\bar{\theta}_{s:t}}) + \int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \\ \mathbf{x}(t) &= \boldsymbol{\mu} + (\mathbf{x}(s) - \boldsymbol{\mu}) \mathrm{e}^{-\bar{\theta}_{s:t}} + \int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \end{aligned} \end{equation}\]which is the solution to the SDE in Eq. \eqref{eq:irsde}. For any starting sample $\mathbf{x}_s$ at time $s$, we can generate the noise-perturbed sample $\mathbf{x}_t$ at time $t$. Looking into the expectation of the Eq. \eqref{eq:solution_irsde}, we have
\[\begin{equation} \begin{aligned} \mathbb{E}[\mathbf{x}(t)] &= \mathbb{E}\left[\boldsymbol{\mu} + (\mathbf{x}(s) - \boldsymbol{\mu}) \mathrm{e}^{-\bar{\theta}_{s:t}} + \int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \right] \\ &= \mathbb{E}\left[\boldsymbol{\mu} + (\mathbf{x}(s) - \boldsymbol{\mu}) \mathrm{e}^{-\bar{\theta}_{s:t}} \right] + \mathbb{E}\left[\int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \right] \\ \end{aligned} \end{equation}\]Since the first part $\mu + (\mathbf{x}(s) - \mu) \mathrm{e}^{-\bar{\theta}_{s:t}}$ is deterministic, its expectation is itself
\[\begin{equation} \mathbb{E}\left[\boldsymbol{\mu} + (\mathbf{x}(s) - \boldsymbol{\mu}) \mathrm{e}^{-\bar{\theta}_{s:t}} \right] = \boldsymbol{\mu} + (\mathbf{x}(s) - \boldsymbol{\mu}) \mathrm{e}^{-\bar{\theta}_{s:t}} \end{equation}\]Regarding the second part $\mathbb{E}\left[\int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \right]$, let’s first review some Itô basics.
Theorem. Let $\mathbf{w}_t$ be a Wiener process, and $\Delta(t)$ be a nonrandom function of time. Suppose that a stochastic process $\mathbf{h}(t)$ satisfies
\[\begin{equation} \mathrm{d} \mathbf{h} = \Delta(z)\mathrm{d}\mathbf{w}_z \\ \mathbf{h}(t) = \int \Delta(z) \mathrm{d}\mathbf{w}_z \end{equation}\]where $\mathbf{h}(0)=0$. Then, for each $t>=0$, the random variable $\mathbf{h}(t)$ is normally distributed.
Let $\Delta(z) = \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}}$ which is nonrandom, $\mathbf{h}(t) = \int_s^t \Delta(z) \mathrm{d} \mathbf{w}_z$, we have
\[\begin{equation} \mathbb{E}\left[\int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \right] = \mathbb{E}\left[\int_s^t \Delta(z) \mathrm{d} \mathbf{w}_z \right] = \mathbb{E}[\mathbf{h}(t)] = \mathbf{0} \end{equation}\]We can further derive the covariance of $I(t)$.
\[\begin{equation} \begin{aligned} \mathrm{Cov}\left(\mathbf{h}(t)\right) &= \mathbb{E} \left[ \left(\mathbf{h}(t)-\mathbb{E}[\mathbf{h}(t)] \right) \left(\mathbf{h}(t)-\mathbb{E}[\mathbf{h}(t)] \right)^\top \right] \\ &= \mathbb{E} \left[ \mathbf{h}(t) \mathbf{h}(t)^\top \right]\\ &= \mathbb{E}\left[ \left(\int_s^t \Delta(z) \mathrm{d} \mathbf{w}_z\right) \left(\int_s^t \Delta(z) \mathrm{d} \mathbf{w}_z\right)^\top \right]\\ \end{aligned} \end{equation}\]Since $\mathbf{h}(t) = \int_s^t \Delta(z) \, \mathrm{d} \mathbf{w}_z$, we can apply the Itô isometry to compute the covariance matrix. For any two components $\mathbf{h}^{(i)}(t)$ and $\mathbf{h}^{(j)}(t)$ of $\mathbf{h}(t)$, we have:
\[\begin{equation} \mathbb{E}\left[ \mathbf{h}^{(i)}(t) \mathbf{h}^{(j)}(t) \right] = \mathbb{E}\left[ \int_s^t \Delta(z) \, \mathrm{d} \mathbf{w}_z^{(i)} \int_s^t \Delta(z) \, \mathrm{d} \mathbf{w}_z^{(j)} \right]. \end{equation}\]Since the Wiener processes $\mathbf{w}_z^{(i)}$ and $\mathbf{w}_z^{(j)}$ are independent for $i \neq j$, the cross terms $\mathbb{E}\left[ \mathbf{h}^{(i)}(t) \mathbf{h}^{(j)}(t) \right] = 0$ when $i \neq j$. For the diagonal terms where $i = j$, the Itô isometry gives:
\[\begin{equation} \mathbb{E}\left[ \left( \mathbf{h}^{(i)}(t) \right)^2 \right] = \mathbb{E}\left[ \left( \int_s^t \Delta(z) \, \mathrm{d} \mathbf{w}_z^{(i)} \right)^2 \right] = \int_s^t \Delta(z)^2 \, \mathrm{d}z. \end{equation}\]Thus, the covariance matrix $\text{Cov}(\mathbf{h}(t))$ is a diagonal matrix, where each diagonal entry is $\int_s^t \Delta(z)^2 \, \mathrm{d}z$.
\[\begin{equation} \begin{aligned} \mathrm{Cov}\left(\mathbf{h}(t)\right) &= \mathbb{E}\left[\left(\int_s^t \Delta(z)^2 \mathrm{d}z\right)\right] \cdot \mathbf{I} \quad (\mathbf{I} \text{ is identity matrix})\\ &= \mathbb{E}\left[\left(\int_s^t \left(\sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}}\right)^2 \mathrm{d}z\right)\right] \cdot \mathbf{I}\\ &= \mathbb{E}\left[\left(\int_s^t \sigma_z^2 \mathrm{e}^{-2\bar{\theta}_{z:t}} \mathrm{d}z\right)\right] \cdot \mathbf{I}\\ &= \mathbb{E}\left[ \frac{\sigma_z^2}{2\theta_z} \mathrm{e}^{-2\bar{\theta}_{z:t}} \bigg|_s^t \right] \cdot \mathbf{I}\\ &= \mathbb{E}\left[ \frac{\sigma_t^2}{2\theta_t} \mathrm{e}^{-2\bar{\theta}_{t:t}} - \frac{\sigma_s^2}{2\theta_s} \mathrm{e}^{-2\bar{\theta}_{s:t}} \right] \cdot \mathbf{I}\\ &= \mathbb{E}\left[ \frac{\sigma_t^2}{2\theta_t} \mathrm{e}^0 - \frac{\sigma_s^2}{2\theta_s} \mathrm{e}^{-2\bar{\theta}_{s:t}} \right] \cdot \mathbf{I}\\ &= \mathbb{E}\left[ \lambda^2 - \lambda^2 \mathrm{e}^{-2\bar{\theta}_{s:t}} \right] \cdot \mathbf{I} \quad (\sigma_t^2 / \theta_t = 2\lambda^2, 0 < t < T) \\ &= \lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{s:t}} \right) \cdot \mathbf{I} \end{aligned} \end{equation}\]Therefore, we have
\[\begin{equation} \mathbf{h}(t) \sim \mathcal{N} \left( \mathbf{0}, \lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{s:t}} \right) \cdot \mathbf{I} \right) \end{equation}\]Note that $\mathbf{x}(t) \sim p_t(\mathbf{x})$ also follows Gaussian distribution:
\[\begin{equation} \begin{aligned} \mathbf{x}(t) &= \boldsymbol{\mu} + \mathrm{e}^{-\bar{\theta}_{s:t}} \cdot \left[ \mathbf{x}(s) - \boldsymbol{\mu} \right] + \int_s^t \sigma_z \mathrm{e}^{-\bar{\theta}_{z:t}} \mathrm{d} \mathbf{w}_z \\ &= \boldsymbol{\mu} + \mathrm{e}^{-\bar{\theta}_{s:t}} \cdot \left[\mathbf{x}(s) - \boldsymbol{\mu} \right] + \mathbf{h}(t) \\ \end{aligned} \end{equation}\] \[\begin{equation} \label{eq:mu_std} \begin{aligned} p(\mathbf{x}(t) | \mathbf{x}(s)) &= \mathcal{N} \left( \mathbf{x}(t) | \boldsymbol{\mu}_{s:t}(\mathbf{x}(s)), \mathbf{\Sigma}_{s:t} \right) \\ \boldsymbol{\mu}_{s:t}(\mathbf{x}(s)) &= \boldsymbol{\mu} + \mathrm{e}^{-\bar{\theta}_{s:t}} \cdot \left[ \mathbf{x}(s) - \boldsymbol{\mu} \right] \\ \mathbf{\Sigma}_{s:t} &= \text{Cov}(\mathbf{h}(t)) = \lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{s:t}} \right)\cdot \mathbf{I} \end{aligned} \end{equation}\]We observe that, with $t \to \infty$, the mean of $\mathbf{x}_t$, $\mu_{s:t}(\mathbf{x}_s)$ converges to the LQ sample $\mu$ and the covariance $\Sigma_{s:t}$ converges to $\lambda^2$, which is called the stationary variance in the IR-SDE paper
Reversing the SDE
By Eq. \eqref{eq:reverse}, the reverse-time SDE corresponding to the SDE (Eq. \eqref{eq:irsde}) is:
\[\begin{equation} \label{eq:reverse_irsde_custom} \begin{aligned} \mathrm{d}\mathbf{x} &= [\mathbf{f}(\mathbf{x}, t) - g(t)^2 \nabla_{\mathbf{x}}\log{p_t(\mathbf{x})}]\mathrm{d}t + g(t)\mathrm{d}\mathbf{\bar{w}} \\ &= \left[ \theta_t (\boldsymbol{\mu} - \mathbf{x}) - \sigma_t^2 \nabla_{\mathbf{x}} \log p_t(\mathbf{x}) \right] \mathrm{d}t + \sigma_t \mathrm{d} \bar{\mathbf{w}} \end{aligned} \end{equation}\]With this reverse-time SDE flowing backwards in time $T \to 0$, we can starting from the LQ sample $\mathbf{x}(T) \sim p_T(\mathbf{x})$ and generate the HQ sample $\mathbf{x}(0) \sim p_0(\mathbf{x})$. However, we still have an unknown part, the score $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$, in the reverse-time SDE.
As the score function $\nabla_{\mathbf{x}} \log p_t(\mathbf{x})$ is intractable for real-world data, it is often approximated by a neural network trained with ground-truth HQ-LQ sample pairs, $\left(\mathbf{x}(0), \mathbf{x}(T)\right)$. To train a neural network mode $s_{\theta}(\mathbf{x}(t), t)$ given time $t$ and the intermediate noisy sample $\mathbf{x}(t)$, we first compute the conditional ground-truth score $\nabla_{\mathbf{x}} \log p_t(\mathbf{x} | \mathbf{x}(0))$ given the HQ sample $\mathbf{x}(0)$. Note that
\[\begin{equation} \label{eq:prob_s_t} p(\mathbf{x}(t) | \mathbf{x}(s)) = \mathcal{N} \left( \mathbf{x}(t) | \boldsymbol{\mu}_{s:t}(\mathbf{x}(s)), \mathbf{\Sigma}_{s:t} \right) \end{equation}\]we have
\[\begin{equation} p_t(\mathbf{x} | \mathbf{x}(0)) = \mathcal{N} \left( \mathbf{x}(t) | \boldsymbol{\mu}_{0:t}(\mathbf{x}(0)), \mathbf{\Sigma}_{0:t} \right) \end{equation}\]To simplify notation, we replace all subscripts $\{ * \}_{0:t}$ with $\{ * \}_{t}$. Thus, we have
\[\begin{equation} \begin{aligned} p_t(\mathbf{x} | \mathbf{x}(0)) &= \mathcal{N} \left( \mathbf{x}(t) | \boldsymbol{\mu}_{t}, \mathbf{\Sigma}_{t} \right) \\ &= \frac{1}{(2 \pi)^{d/2} |\mathbf{\Sigma}_{t}|^{1/2}} \exp\left( -\frac{1}{2} \left(\mathbf{x}(t) - \boldsymbol{\mu}_{t}\right)^\top \mathbf{\Sigma}_{t}^{-1} \left(\mathbf{x}(t) - \boldsymbol{\mu}_{t}\right) \right) \end{aligned} \end{equation}\]Hence, the score has the following closed-form solution:
\[\begin{equation} \nabla_{\mathbf{x}} \log p_t(\mathbf{x} | \mathbf{x}(0)) = -\mathbf{\Sigma}_{t}^{-1} \left( \mathbf{x}(t) - \boldsymbol{\mu}_{t} \right) \end{equation}\]Training Objectives
Noise Prediction
With ground-truth clean sample $\mathbf{x}(0)$ in training, we first perturbe $\mathbf{x}(0)$ through the diffusion process via the forward SDE and obtain the noise-perturbed sample $\mathbf{x}(t)$.
Next, we compute the mean $\mu_{t}$ and covariance $\Sigma_{t}$ by Eq. \eqref{eq:mu_std} such that we can obtain the ground-truth score $\nabla_{\mathbf{x}}\log{p_t(\mathbf{x}|\mathbf{x}(0))}$ for training the score network $\mathbf{s}_{\theta}(\mathbf{x}(t),t)$.
During inference, the reverse-time SDE starts from the final time $T$ such that the score network approximates the score at time $T$ given the most noisy input LQ sample, $\mathbf{x}(T)$. Ideally, after iteratively running backwards in time, $T \to 0$, the reverse process will generate the clean HQ sample, $\mathbf{x}(0)$, via the reverse-time SDE (Eq. \eqref{eq:reverse_irsde_custom}). However, the actual performance might not be as expected, as detailed in many studies.
Considering the conditional distribution, $p_t(\mathbf{x} | \mathbf{x}(0)) \sim \mathcal{N}(\mu_t, \Sigma_t)$, we have $\mathbf{x}(t) = \mu_{t} + |\Sigma_t|^{1/2} \epsilon_t$, where $\epsilon_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$. The score is reparameterized as
\[\begin{equation} \nabla_{\mathbf{x}} \log p_t(\mathbf{x} | \mathbf{x}(0)) = -\mathbf{\Sigma}_{t}^{-1/2} \boldsymbol{\epsilon}_t \end{equation}\]Therefore, we can, instead, train a noise network $\tilde{\epsilon}_{\phi}(\mathbf{x}(t), \mu, t)$ which takes the intermediate noisy sample $\mathbf{x}(t)$, the LQ sample or condition $\mu$, and the time $t$ as input and outputs the noise to approximate the ground-truth noise $\epsilon_t$.
The noise network can be trained following a similar framework proposed in the work Denoising Diffusion Probabilistic Models (DDPM)
where, for the $i^{\text{th}}$ step in the diffusion process, $\gamma_i$ denotes the weight, $\mathbf{x}_i$ represents the intermediate noisy sample, and ${\epsilon}_i$ is the ground-truth randomly sampled Gaussian noise.
After the noise network $\tilde{\epsilon}_{\phi}(\mathbf{x}_i, {\mu}, i)$ is trained, we can start from the LQ sample $\mathbf{x}_N$ and iteratively solve the reverse-time SDE with numerical approaches (e.g., Euler-Maruyama or stochastic Runge-Kutta methods) for generating the HQ sample $\mathbf{x}_0$. More details can be found in the study, Score-based Diffusion Models through SDE
Maximum Likelihood
Unfortunately, the above objective $L_{\gamma}(\phi)$ did not produce good HQ samples in experiments while there is not good reason in the original paper explaining this issue. Instead, a new maximum likelihood objective was proposed for training the noise network.
In this part, let’s the diffusion process at discrete times $\{i\}_{i=0}^N$ and the Markov property. The joint probability of $(\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_N )$ conditioned on $\mathbf{x}_0$ is
\[\begin{equation} p(\mathbf{x}_{1:N}|\mathbf{x}_0) = p(\mathbf{x}_N|\mathbf{x}_0) \prod_{i=2}^N p(\mathbf{x}_{i-1}|\mathbf{x}_{i}, \mathbf{x}_0) \end{equation}\]where we consider the intermediate noisy sample $\mathbf{x}_{i-1}$ is conditioned on both the initial HQ sample $\mathbf{x}_0$ and the next noise-perturbed sample $\mathbf{x}_{i}$.
Using Bayes’ rule, the reverse transition, $p(\mathbf{x}_{i-1} | \mathbf{x}_i, \mathbf{x}_0)$ can be expressed as
\[\begin{equation} \begin{aligned} p(\mathbf{x}_{i-1}|\mathbf{x}_{i}, \mathbf{x}_0) &= \frac{p(\mathbf{x}_{i}|\mathbf{x}_{i-1}, \mathbf{x}_0) p(\mathbf{x}_{i-1}|\mathbf{x}_0)}{p(\mathbf{x}_i|\mathbf{x}_0)} \\ &= \frac{p(\mathbf{x}_{i}|\mathbf{x}_{i-1}) p(\mathbf{x}_{i-1}|\mathbf{x}_0)}{p(\mathbf{x}_i|\mathbf{x}_0)} \end{aligned} \end{equation}\]where each of the above probabilities are Gaussian (Eq. \eqref{eq:prob_s_t}). The goal is to find the optimal $\mathbf{x}_{i-1}^*$ to maximize the likelihood $p(\mathbf{x}_{i-1} | \mathbf{x}_i, \mathbf{x}_0)$ or minimize the negative log likelihood (NLL) $- \log p(\mathbf{x}_{i-1} | \mathbf{x}_i, \mathbf{x}_0)$.
\[\begin{equation} \begin{aligned} \mathbf{x}_{i-1}^* &= \arg \max_{\mathbf{x}_{i-1}} \left[ p(\mathbf{x}_{i-1}|\mathbf{x}_{i}, \mathbf{x}_0)\right] \\ &= \arg \max_{\mathbf{x}_{i-1}} \left[ p(\mathbf{x}_{i}|\mathbf{x}_{i-1}) p(\mathbf{x}_{i-1}|\mathbf{x}_0) \right] \\ &= \arg \min_{\mathbf{x}_{i-1}} \left[ -\log p(\mathbf{x}_{i}|\mathbf{x}_{i-1}) - \log p(\mathbf{x}_{i-1}|\mathbf{x}_0) \right] \\ \end{aligned} \end{equation}\]The discretized version of the transition kernel, $p(\mathbf{x}_t | \mathbf{x}_s)$, between times $s$ and $t$, becomes:
\[\begin{equation} \label{eq:prob_s_t_discrete} \begin{aligned} p(\mathbf{x}_t | \mathbf{x}_s) &= \mathcal{N} \left( \mathbf{x}_t | \boldsymbol{\mu}_{s:t}(\mathbf{x}_s), \mathbf{\Sigma}_{s:t} \right) \\ \boldsymbol{\mu}_{s:t}(\mathbf{x}_s) &= \boldsymbol{\mu} + \mathrm{e}^{-\bar{\theta}_{s:t}} \cdot \left[ \mathbf{x}_s - \boldsymbol{\mu} \right] \\ \mathbf{\Sigma}_{s:t} &= \text{Cov}(\mathbf{h}_t) = \lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{s:t}} \right)\cdot \mathbf{I} \end{aligned} \end{equation}\]As the transitions $p(\mathbf{x}_{i} | \mathbf{x}_{i-1})$ and $p(\mathbf{x}_{i-1} | \mathbf{x}_0)$ have been derived in Eq. \eqref{eq:prob_s_t_discrete}, we can solve the above optimization problem by taking the derivative.
\[\begin{equation} \begin{aligned} & - \nabla_{\mathbf{x}_{i-1}} \log p(\mathbf{x}_{i}|\mathbf{x}_{i-1}) - \nabla_{\mathbf{x}_{i-1}} \log p(\mathbf{x}_{i-1}|\mathbf{x}_0) \\ = & - \mathbf{\Sigma}_{(i-1):i}^{-1} (\mathbf{x}_{i} - \boldsymbol{\mu}_{(i-1):i})\mathrm{e}^{-\bar{\theta}_{(i-1):i}} - \mathbf{\Sigma}_{0:(i-1)}^{-1} (\mathbf{x}_{i-1} - \boldsymbol{\mu}_{0:(i-1)}) \\ = & -\frac{\mathrm{e}^{-\bar{\theta}_{(i-1):i}}}{\lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{(i-1):i}} \right)} (\mathbf{x}_{i} - \boldsymbol{\mu} - \mathrm{e}^{-\bar{\theta}_{(i-1):i}} \cdot ( \mathbf{x}_{i-1} - \boldsymbol{\mu} )) \\ & +\frac{1}{\lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{0:(i-1)}} \right)} (\mathbf{x}_{i-1} - \boldsymbol{\mu} - \mathrm{e}^{-\bar{\theta}_{0:(i-1)}} \cdot \left( \mathbf{x}_0 - \boldsymbol{\mu} \right)) \\ = & 0 \end{aligned} \end{equation}\]Setting the above derivative to 0 and solving the equation, we have:
\[\begin{equation} \mathbf{x}_{i-1}^* = \frac{1- \mathrm{e}^{-2\bar{\theta}_{0:(i-1)}}}{1- \mathrm{e}^{-2\bar{\theta}_{0:i}}} \mathrm{e}^{-\bar{\theta}_{(i-1):i}} (\mathbf{x}_{i}-\boldsymbol{\mu}) + \frac{1- \mathrm{e}^{-2\bar{\theta}_{(i-1):i}}}{1- \mathrm{e}^{-2\bar{\theta}_{0:i}}} \mathrm{e}^{-\bar{\theta}_{0:(i-1)}} (\mathbf{x}_{0}-\boldsymbol{\mu}) + \boldsymbol{\mu} \end{equation}\]Given that the second-order derivative with respect to $\mathbf{x}_{i-1}$ is positive:
\[\begin{equation} \frac{\mathrm{e}^{-2\bar{\theta}_{(i-1):i}}}{\lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{(i-1):i}} \right)} + \frac{1}{\lambda^2 \left( 1- \mathrm{e}^{-2\bar{\theta}_{0:(i-1)}} \right)} > 0 \end{equation}\]The solution $\mathbf{x}_{i-1}^*$ is a global optimal.
—–The End—–